Finding Triangular Configuration of Matrices

This section seeks to explore triangular matrices and their specific structure. Triangular matrices are particularly useful for quicker row reduction using forward or backward substitution. This algorithm takes in a matrix as input, and determines if its rows can be rearanged to yeild a triangular matrix in any of the 4 forms. If a configuration does not exist, " No Triangular Configurations Exist!" is returned.

Process

    1. First check is the matrix is square, meaning its number of rows equal its number of columns
    2. Next create an array of row indices (three rows implies our array is [1,2,3] )
    3. Use Python's itertools library to find all possible permutations of this array
    - [1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,2,1],[3,1,2] (notice the number of arrangements is 3!)
    4. Next,loop through each row arrangement of the matrix as given by each permutation
    5. Check if either diagonals contain only nonzero entries as that is a key criteria of triangular matrices
    6. Determine if the matrix is Lower Left, Lower Right, Upper Left, Upper Right Triangular
    7. Return the matrix configuration that has the row arrangement corresponding to the array of indices

Example

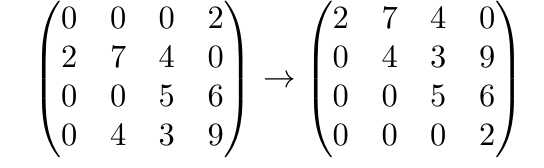
  • Notice the original indices, [1,2,3,4], are then mapped to [2,4,3,1] and "Upper Right Triangular" is returned

    • Tools Used

  • Python
  • Python itertools and permutations